본 포스팅은 교통 공학자가 최적화 방법론을 활용한 연구를 진행하기 위해 필요한 선행 지식들 (1) 최적화 식 포뮬레이션 방법, (2) 복잡한 문제의 근사법과 해결법 (3) 솔버 추천, 구현 및 디버깅 방법 을 다룹니다.
Prerequisite.
- 최적화 문제의 구성 요소 (결정변수, 목적함수, 제약식) 에 대해 알고 있다.
- Optimal solution, lower bound, upper bound 가 무엇인지 알고 있다.
- Linear programming 과 Convex programming 의 standard form 에 대해 알고 있다.
최적화 식 포뮬레이션.
기본적으로 최적화의 기초를 알고 있고 decision variables, objective function, constraints 이 무엇인지 설명할 수 있지만 막상 내가 풀고싶은 문제를 포뮬레이션 하려니 어려움을 느끼신 적 있으신가요? 제가 생각하는 한가지 좋은 공부 방법은 예제를 잡고 그 포뮬레이션이 어떻게 구성되었나를 깊이 있게 이해하는 것입니다.
Vehicle Routing Problem with Time Window (VRPTW) 는 잘 알려진 combinatorial optimization 문제입니다. 포뮬레이션이 쉽지 않은 이유는 같은 상황을 수식으로 어떻게 표현하냐에 따라서 문제의 복잡도와 해결법이 달라지기 때문인 것 같습니다. 아래 책에 같은 문제를 표현할 수 있는 두가지 방식의 포뮬레이션 (arc-flow formualtion 과 path-flow formulation) 이 설명되어있습니다.
https://epubs.siam.org/doi/10.1137/1.9781611973594.ch5
문제가 어떻게 정의되었는지, 즉 주어진 상황과 값은 무엇이고 어떤것을 결정하고자 하는지 파악한 후, 결정 변수가 어떻게 정의되었고 목적함수는 어떻게 정의되었으며, 현실 상황을 모사하기 위한 제약식은 어떻게 적혀있는지 살펴보면 감이 올 것입니다. 포뮬레이션 할때에는 복잡도를 계산하는 방법을 알아야합니다. 문제의 복잡도는 변수의 개수와 제약식의 개수로 정의됩니다.
문제를 더 쉽게 바꾸기 위한 여러가지 relaxation 방법을 고려해 볼 수 있습니다. 책에 소개된 Big-M relaxation 이라는 예시를 들어보겠습니다.

위 제약식 하나때문에 전체 문제가 nonlinear 해집니다. 이를 linearize 하기 위해 Big-M relaxation 을 고려해볼 수 있습니다. 일반적으로 Big-M relaxation 은 weak lower bound 를 가진다고 알려져 있기 때문에 주의해야합니다.

쉬운 수식이지만 이를 떠올리기는 쉽지 않을 수 있습니다. 개인적인 생각으로는 이런 트릭에 대한 아이디어들을 얻기 위해서는 본인이 풀고자하는 문제의 선행 연구들의 포뮬레이션을 많이 참고하는 것이 가장 좋은 방법인 것 같습니다.
추가로 포뮬레이션을 그대로 구현하려는 과정에서도 어려움을 겪을 수 있습니다. 아래 포스팅을 보면 위 책에 나온 포뮬레이션을 그대로 구현해보려고 시도한 사람이 Request size 25명 정도로 작은 문제를 다루는데도 optimality gap 이 크다고 말한 것을 알 수 있습니다.

답변을 보면 state-of-the-art 는 branch-prize-and-cut 방법이 가장 좋은 해를 준다고 알려져 있다고 합니다. 각 문제에서 현존하는 가장 좋은 방법이 무엇인지 알기 위해서는 선행 연구 조사가 가장 좋은 방법이라고 생각합니다.
복잡한 문제의 근사법과 해결법.
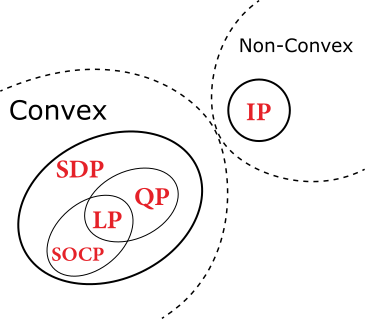
이처럼 포뮬레이션이 어려운 이유는 같은 문제를 표현할 수 있는 여러 가지의 포뮬레이션이 존재하기 때문입니다. 여러가지의 포뮬레이션 중 좋은 포뮬레이션이라고 하면 "풀기 쉬운" 문제 일 것 입니다. 아래 제시된 topology 에서 더 작은 동그라미에 속할 수록 더 풀기 쉬운 문제입니다.
내 포뮬레이션이 어떤 문제에 속하는지 확실하게 판단할 수 있는 방법은 standard form 적어 보는 것입니다. LP, IP, Convex programming 의 standard format 정도는 기본적으로 알아두면 좋습니다.
솔버 추천.
솔버를 선택하는 것 조차도 생각보다 쉽지 않은 문제입니다. 개인적으로는 linear 혹은 integer program 을 다룰때는 Gurobi, Convex 문제를 다룰 때에는 MOSEK 를 주로 활용합니다. 모두 무료로 아카데믹 라이센스를 받을 수 있습니다. 학계에서 좋다고 평가받는 몇개의 솔버가 있지만 문제별로 성능이 어떨지는 구현해보기전에 정확히 예측하기 쉽지 않습니다. 이와 같은 맥락에서 Julia 라는 프로그래밍 언어를 배우는 것을 강력 추천합니다. (1) C++ 만큼 빠르고 python 만큼 쉬우며 (2) 여러 솔버의 전환이 하나의 커멘드 라인 만으로 가능합니다.
대부분의 교통 문제를 그래프를 포함하기 때문에 처음에는 어떻게 구현하는 것이 좋을지 막막하게 느껴질 수 있습니다. Gurobi 나 홈페이지에 꽤나 많은 교통 문제 예제를 찾을 수 있습니다.
https://www.gurobi.com/jupyter_models/
Jupyter Models Archive - Gurobi Optimization
Advanced These modeling examples assume that you know Python and the Gurobi Python API and that you have advanced knowledge of building mathematical optimization models. Typically, the objective function and/or constraints of these examples are complex or
www.gurobi.com

구현 및 디버깅.
포뮬레이션이 맞았는지 틀렸는지 확인해보는 방법은 실제로 구현해 보는 것입니다. 이때 목표로 하는 네트워크에 바로 적용하는 것 보다는 단계별로 구현하는 방식이 좋습니다. 저의 경우에는 toy network > Benchmark network > 실제 교통 네트워크 (osmnx) 순서로 적용해보는 편이고, 귀찮아도 시각화를 최대한 많이 해보는 편입니다.
Logging file 을 해석하는 것도 중요합니다.
'석박사 > 최적화는 사기가 아니얏!' 카테고리의 다른 글
| Gurobi 로그 파일 시각화 (log file visualization) (0) | 2023.11.16 |
|---|---|
| Gurobi Constraint Matrix Format 으로 작성하기 (0) | 2023.11.09 |
| Operations Research Cheat Sheet Technical Interview (0) | 2023.01.30 |
| nonlinear convex optimization을 푸는 CVXOPT 솔버 (0) | 2022.11.29 |
| VRP state-of-the-art solver - LKH, HGS (0) | 2022.10.23 |


