사전 지식
active 하다는 것? 만일 어떤 벡터가 제약식의 equality 를 만족하면 그 제약식은 active 혹은 binding 되었다고 한다. 직관적으로 크거나 같다/ 작거나 같다 등의 조건이 있을때 그 조건에 딱 걸쳐있는 벡터를 상상하면 쉽다.
Basic solution 이란?
어떤 벡터가 basic solution 이 될 조건은? (차원이 n 이라고 하자)
(1) active contraints 중 선형 독립이 n개 존재해야 함. (n은 차원의 수)
(2) equality contrains 은 무조건 active 해야함.
첫번째 조건은 직관적으로 이해가 된다. solution을 어떤 한 점이라고 생각한다면 2차원의 공간에서 한 점을 특정하기위해서는 2개의 선분이 필요할테고 3차원의 공간에서 한 점을 특정하기 위해서는 3개의 평면이 필요할 것이다. 이렇듯 n 차원의 공간에서는 n 개의 선형 독립인 n 개의 active constraint 가 필요하다. 두번째 조건은 한번에 무슨뜻인지 이해하기도 어렵고 깜빡하기도 쉽다. 이를 이해하기 위해 아래 예시를 살펴보자. 다음 3차원 공간에 총 4개의 제약식이 존재하는 상황을 생각해보자. 다음과 같이 한개의 equality constraint 와 3개의 inequality constraints 가 있다.
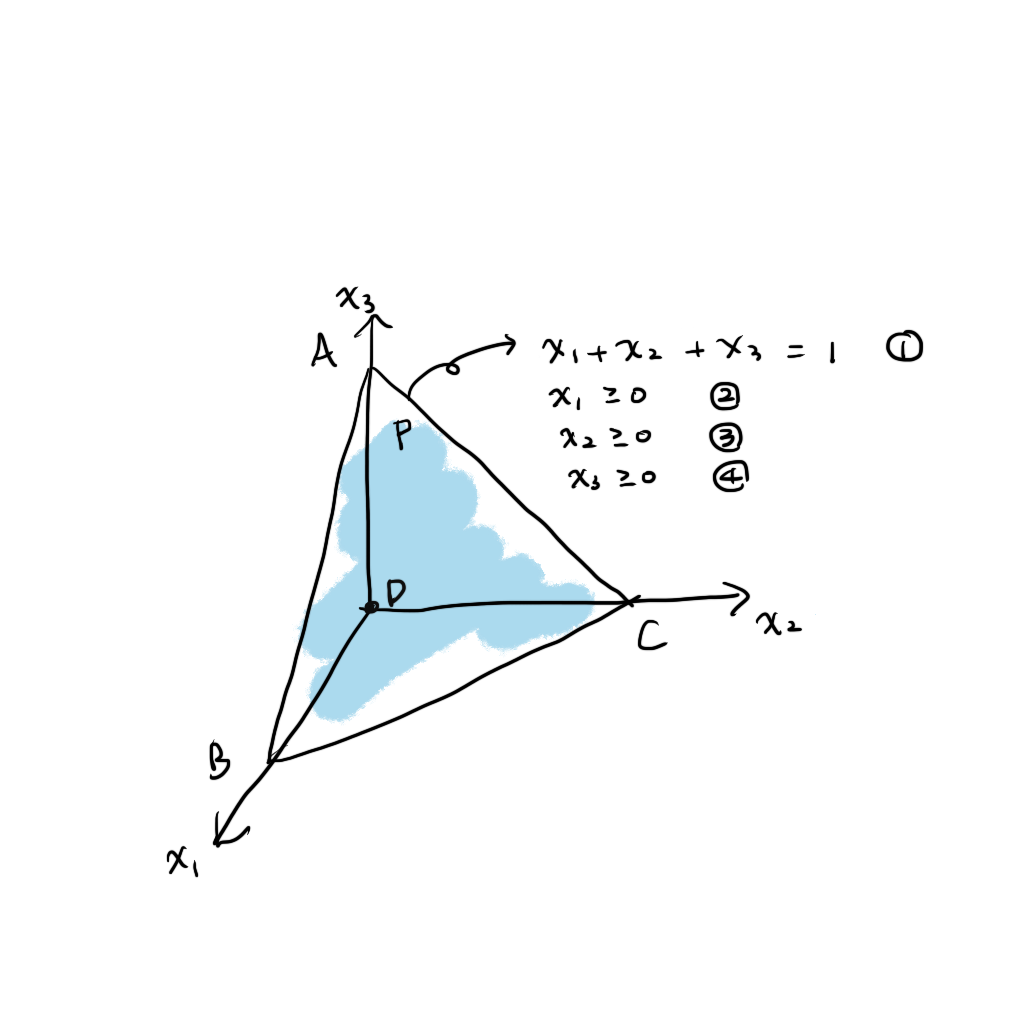
이 중 3개의 제약식이 active 한 경우는 A, B, C, D 이다.
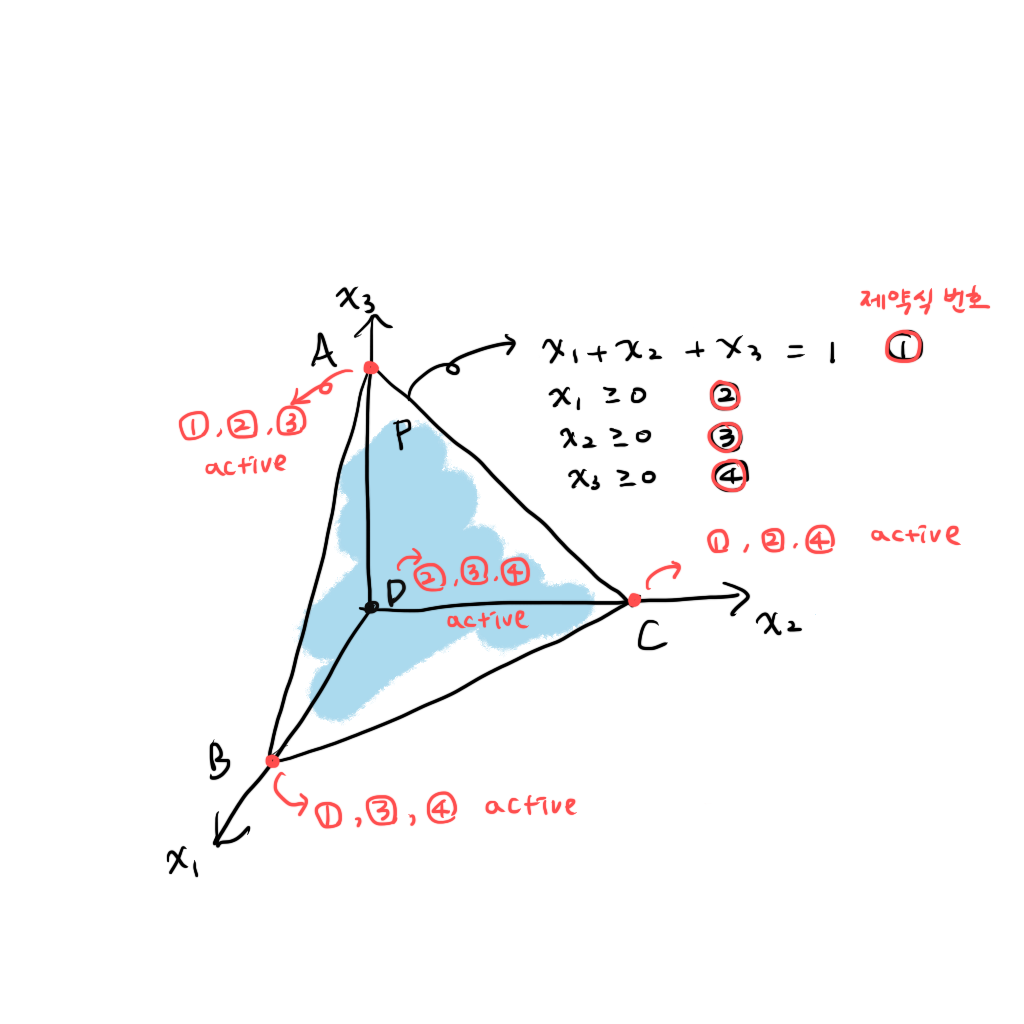
3개의 제약식이 존재하지 않는 점을 하나만 예시로 들어보면 E가 있다. E에서는 1번과 3번, 총 2개의 제약식만이 active 하고 그 두개의 제약식을 만족하는 점은 그림에 표시된 E로 특정되지 않으며 AB 선분 상의 어느 점이나 될 수 있다.
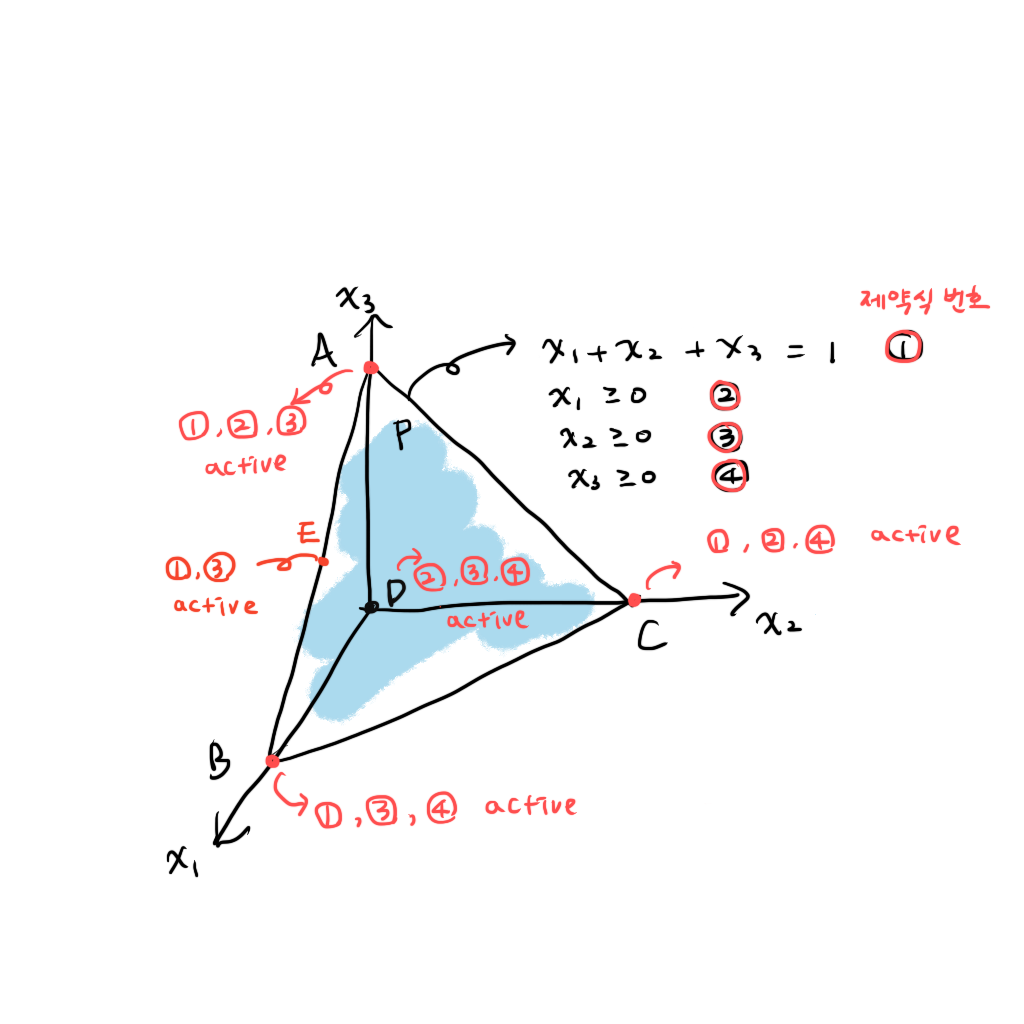
한가지 주의할 점은 equality constraint 는 무조건 active 해야한다는 점이다. 1번 제약식이 active 한 A,B,C와는 다르게 D는 basic solution 이 아니다.
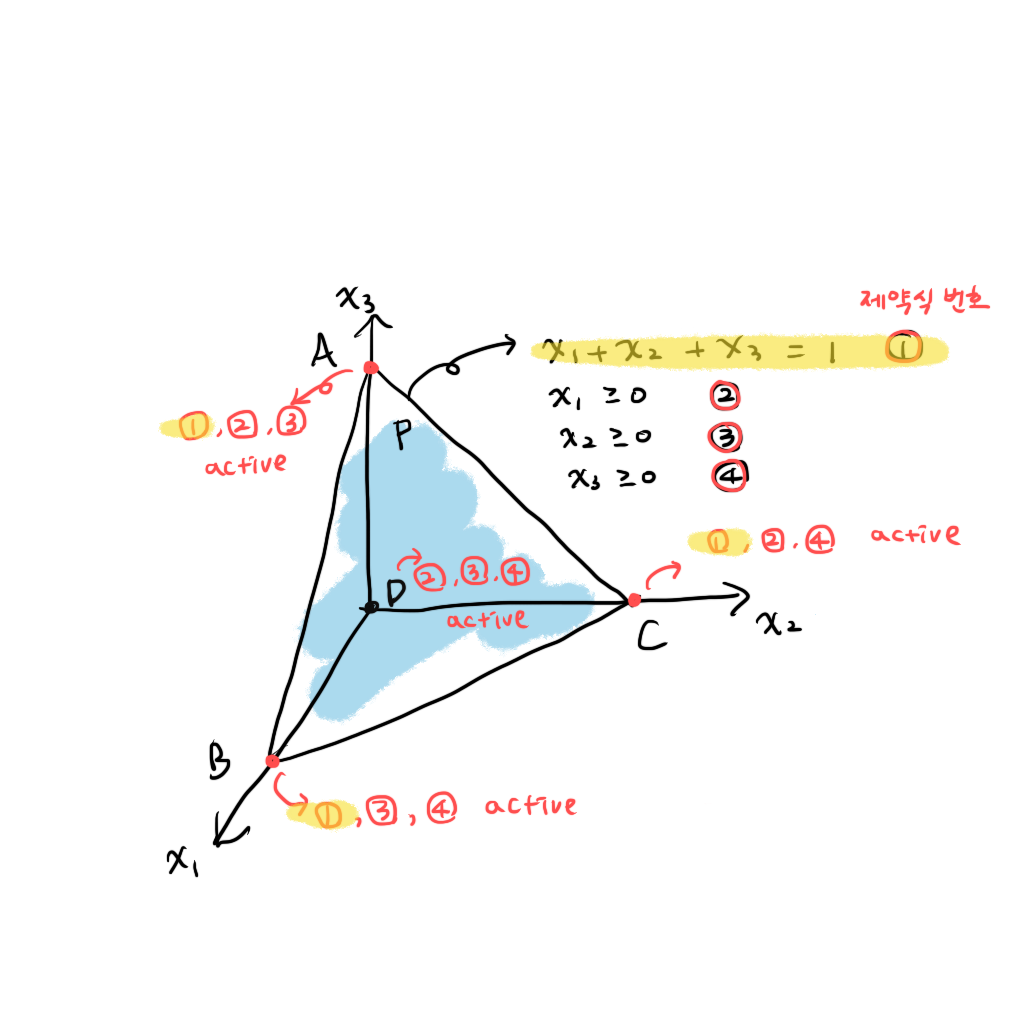
Basic feasible solution 이란?
만약 basic solution 이 존재하는 모든 제약식들을 만족시킨다면 그것은 basic feasible solution이다. A, B, C 는 4개의 제약식을 모두 만족하므로 basic solution이자 basic feasible solution이다.
이 예시만 놓고 살펴보면 basic solution이지만 basic feasible solution 이 되지 않는 경우가 궁금해질 것이다. 조금 더 단순한 2차원의 예시를 보자. 이 예시에서는 inequality constraint 만 존재한다.
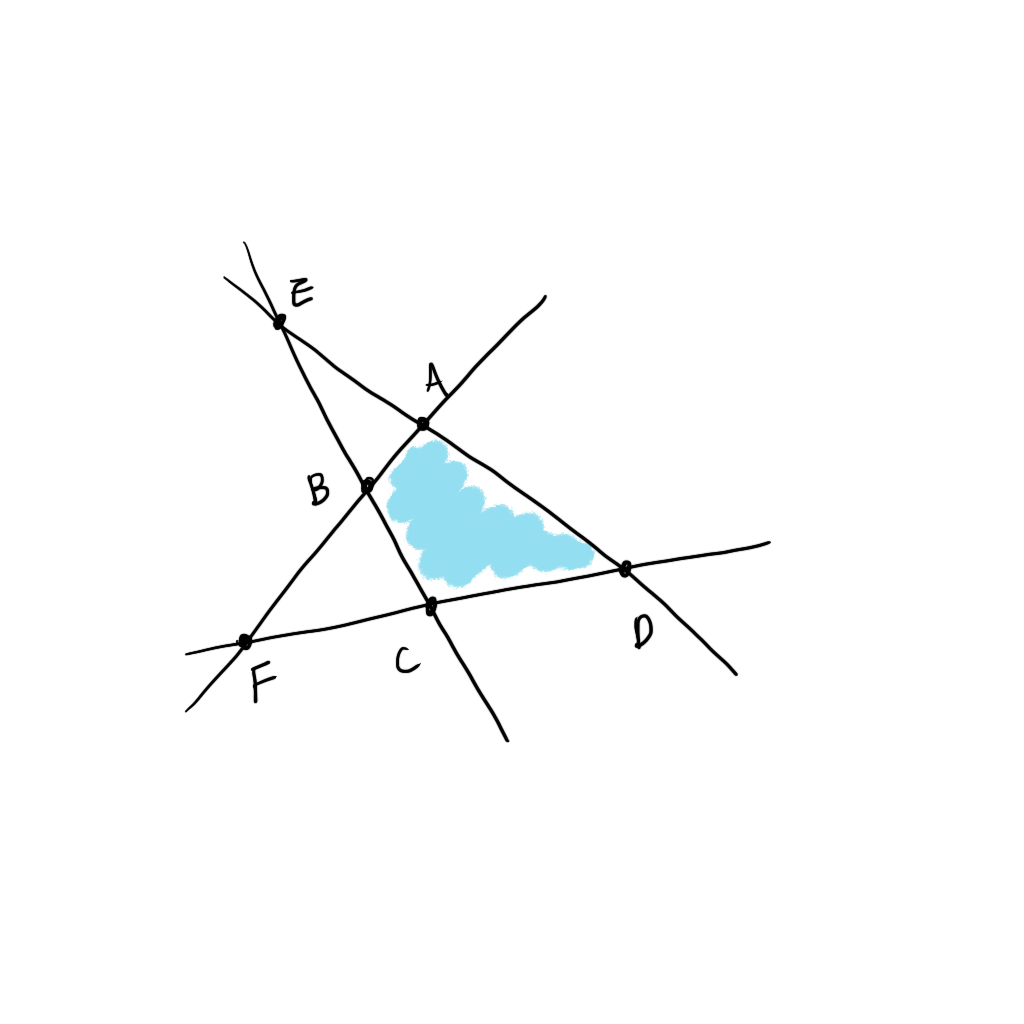
A, B, C, D, E, F 모두 2개의 제약식이 만나는 곳이다. E, F는 모든 제약식을 만족하지는 않는다. (직관적으로 어떤 지점이 제약식을 만족하지 않는다는건 우리의 제약식 하에서 불가능한 경우라는 뜻이다) 따라서 이 경우 E, F 는 basic solution 이지만 feasible 하지는 않다.
| basic solution | basic feasible solution | |
| A, B, C, D | O | O |
| E,F | O | X |
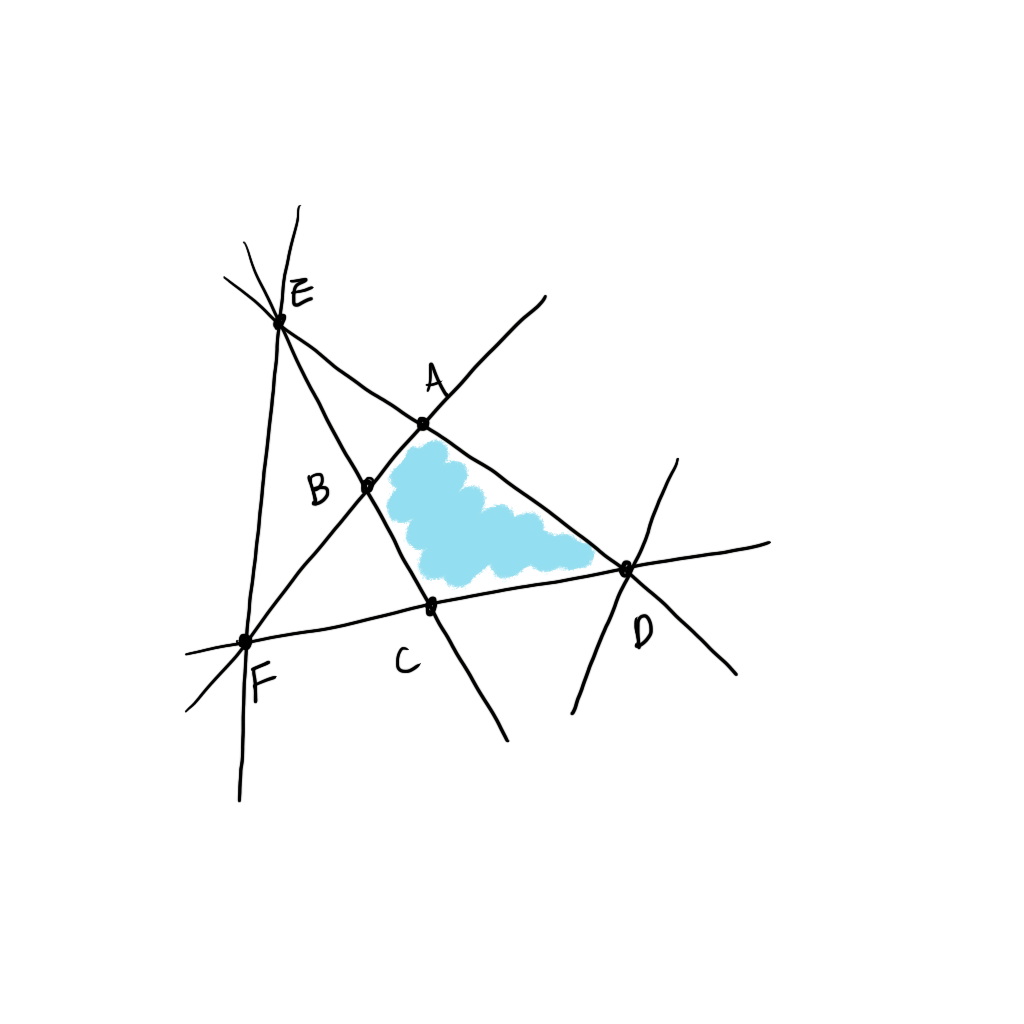
조금 더 복잡한 상황을 생각해보자. 위의 예시에서 제약식을 두개 더 추가해보았다. 이제 E, F와 D 에서는 3개의 벡터가 만난다. 2차원의 공간에서 한 점을 특정하기 위해서는 두개의 벡터만 있으면 되는데 필요한 것보다 많은 벡터가 있는 것이다. 우리는 이처럼 n 차원에 존재하는 basic solution 에서 n개보다 많은 active constraints가 있을 때 이를 degenerate 하다고 한다.
E와 F는 degenerate basic solution 라 하며, D는 degenerate basic feasible solution 이라 한다.
Basic feasible solution 이 왜 중요한가?
만약 유한한 개수의 제약식이 존재한다면 basic feasible solution도 유한개만 존재할 수 밖에 없다. 따라서 직관적으로 basic feasible solution을 모두 찾아 그것의 최소/최대값을 구하면 그것이 우리가 원하는 optimal solution일 것임을 알 수 있다. 이 포스팅에서는 직관적으로 이해하기 쉽게 하기 위해 기하학적인 것 위주로 설명을 했는데 실제로 문제를 풀때는 컴퓨터에 입력을 해주어야하므로 대수적인 관점으로 문제가 바뀐다. 별건아니고 그냥 equality constraint은 반드시 만족하면서 전체 active 한 constraints의 개수가 총 n 개가 되도록 제약식을 뽑아온 다음 연립방정식의 해를 구해내는 과정이다.
하지만 유한개라 할지라도 그 크기가 너무 크면 (exponentially large) 하면 현실적으로 다항시간내에 푸는 것이 불가능할 것이다. 이를 효율적으로 찾아 나가는 방법이 simplex method 이며 나중에 다룰 것이다.
'일기 > 수업 필기 노트' 카테고리의 다른 글
| 튜링머신에 대한 완벽한 이해 (1편) (0) | 2020.11.06 |
|---|---|
| decision problem 과 optimization problem 의 관계 (feat. np) (0) | 2020.11.03 |
| Duality 변환 공식 암기하지말고 이해하기 (1) | 2020.10.21 |
| Lagrange Multiplier 로 유도해보는 dual (0) | 2020.10.21 |
| simplex method와 cycling 극복법 (0) | 2020.10.21 |