LeetCode 라는 사이트에서 준비하면 된다. 랜덤한 문제를 골라 푸는 것 보다 스터디 플랜을 선택하는게 낫다. 우버 면접 경험이 있는 친구는 Algorithm 1, 2 정도 공부하면 충분하다고 했다.
커버해야하는 문제들은 다음과 같이 유형화 할 수 있다. 실제 인터뷰에서는 주어진 문제를 읽고 어떤 유형의 문제인지 파악하는 것 부터가 시작이기 때문에 어떤 유형들이 있는지 머리속에 넣어두면 좋다.
- Binary search
- Two pointers
- Sliding window
- Breadth-First search, Depth-First search
- Recursion/Backtracking
- Dynamic Programming
- Bit Manuplation
Big-O notation 이해하기
솔루션을 생각해내는 것 보다 중요한 것은 그 솔루션의 time and space complexity 를 생각해내는 것이다. 기본적으로 instance 사이즈가 n 으로 주어졌을때 worst case scenario 의 경우 몇번의 탐색 과정을 거쳐 솔루션을 구해낼 수 있을지에 대한 것이다. 꽤나 big-O notation 에 익숙하다고 생각했었는데 mock interview 를 진행하는 인터뷰 비디오를 보다가 왜 binary search 가 log n 인지 물어보는 질문이 나왔는데 좀 당황스러웠다. reasoning 은 binary search를 진행하면 각각의 recursive 스텝에서 탐색 범위를 n, n/2, n/4, ... n/(2^k) 개로 줄여나갈 수 있다. k 스텝 후에는 n/(2^k)<=1 가 되는 k 를 원할 것이고 이는 log_2(n) <=k 라는 식을 이끌어낸다.
Data Structure & Algorithm Basics
기본 데이터 스트럭쳐에 대한 것을 이해해야한다. 아래 설명중 이해가 안되는 문장이 있다면 구글링을 통해 공부하는것을 권한다. 면접 전에 알아야하는 기본 개념이다. 이 글의 독자는 Big-O 노테이션을 알고있다고 가정한다.
array (혹은 list) 는 indexing 에는 최적이다 (e.g. list[i] 해서 i 번째 인덱스에 저장된 값을 가져오는것). 하지만 값이 주어졌을때 해당되는 인덱스를 찾는 것 (searching) 에는 효율이 좋지 못하다. 순서대로 값을 찾는다면 O(n). 따라서 O(log n) 의 연산시간을 가져다 줄 수 있는 binary search 가 중요하다.
특정 index 에 insertion 하면 그 이후 모든 값들의 인덱스가 하나씩 밀려야하고, 마찬가지로 deleting 하면 모든 인덱스가 하나씩 당겨진다. 따라서 insertion, deleting 은 O(n) 임을 유의해야한다. 이 단점을 극복할 수 있는 Linked List 라는 데이터 스트럭쳐의 개념을 아는게 중요하다. Linked list 는 searching 과 indexing 이 O(n) 이지만 insertion/deleting 이 O(1) 이다.
Stack 과 Queue 는 array 로 구현 가능한데, stack 은 last in first out 원칙으로 DFS 에 사용되고, queue 는 first in first out 원칙으로 BFS 에 사용된다. BFS, DFS 는 O(V+E) 이다 (V는 node 개수, E는 edge 개수). stack 은 마지막 요소의 pointer 만 가지고 있어도 되는 반면 queue는 처음과 맨 끝, 두개의 pointers 를 가져야하기 때문에 stack 이 메모리를 덜 먹는다. 따라서 어차피 모든 경우를 탐색해야하는 경우라면 dfs 가 더 나은 선택이다. 아래 코드를 보면 stack 과 queue 모두 list 로 정의할 수 있고 pop() 함수를 이용하면 디폴트로는 맨 마지막 값을 리턴하고 pop(0)을 하면 맨 처음 값을 리턴하는데 O(n) 연산이라 비효율적이다. 효율성을 높이기 위해서는 double-ended-queue (Deque, 데크)를 이용한다.
stack = [1, 2]
stack.append(3)
# Removes the last item
stack.pop()
from collections import deque
queue = deque([1, 2])
queue.append(3)
queue.popleft()Hash map/Hash table 은 쉽게말해 파이썬의 dictionary 에 해당한다. "hashing" 한다고 말하면 key 값을 가지고 일대일 대응이 되는 value 를 찾는다는 말이다. Hash function 은 data/object 의 고유한 메모리 값을 반환한다. indexing, searching, insertion 이 모두 O(1)이다.
실전 연습
https://www.youtube.com/watch?v=SKLyXWhtSo0
면접 전날 이 동영상을 보면서 실전 감을 쌓았다. 그간 연습했던 문제보다 훨씬 쉬웠는데 오히려 어려운 파트는 문제를 본 순간 든 솔루션을 영어로 설명하고, 복잡도를 말하고, 솔루션을 어떻게 개선해나갈지에 대한 생각을 말하는 파트라는 생각이 들었다. 유형별로 high level solution 을 영어로 설명하는 스크립트가 필요했다. 예를들면,
BFS traverses the graph in a breadthwise direction, layer by layer. It move horizontally and visit all the nodes in the current layer and continue to the next layer. BFS uses a queue which operates based on the first in first out principle. To explain the pseudo code in a high level, I will firstly initialize the queue with a root node. While any element in the queue exists, I’ll pop out the first element and store it’s children nodes to additional array so that we can keep track of what would be the nodes that we need to search in the next layer. I’ll keep iterating until the current queue runs out every elements, and replace the empty queue to the additional array.
DFS starts at the root node and explores as far as possible along each branch before backtracking. DFS uses a stack which operates based on last in first out principle.
유형별 문제 공략
면접 직접, 내가 지금까지 푼 문제들을 다시 복습하면서 더 나은 코드가 없었나 다시 고민해보았다. 패턴마다 처음에 접근하는 방식이 정해져있어서 그 툴을 사용해서 문제를 생각해보고 문제가 변형되었다면 무엇이 문제를 어렵게 만드는지 생각해봐야한다. 바로 코드를 써내려가기보단 문제를 읽고 주어진 예제를 활용해 노트를 적어가면서 충분히 생각해나가는게 유리하다. 생각을 너무 복잡하게 하고있다면 단순하게 알고있는 패턴을 적용할 순 없을지 따져보면 생각보다 간단한 코드로 풀리는 경우가 많았다.
Binary search
바이너리 서치가 아이디어는 쉬운데 은근 생각하는게 까다롭다. while 문으로 짜서 lo, hi 를 계속 업데이트 해나가야한다는것 (recursion 사용하면 코드가 꼬이는것을 여러번 느꼇다), 한 while 루프를 돌았는데 구간이 그대로인 상황이 있어서는 안된다는 것, 탐색 범위를 절반씩 줄여나가야 한다는 것이다.
704. Binary Search
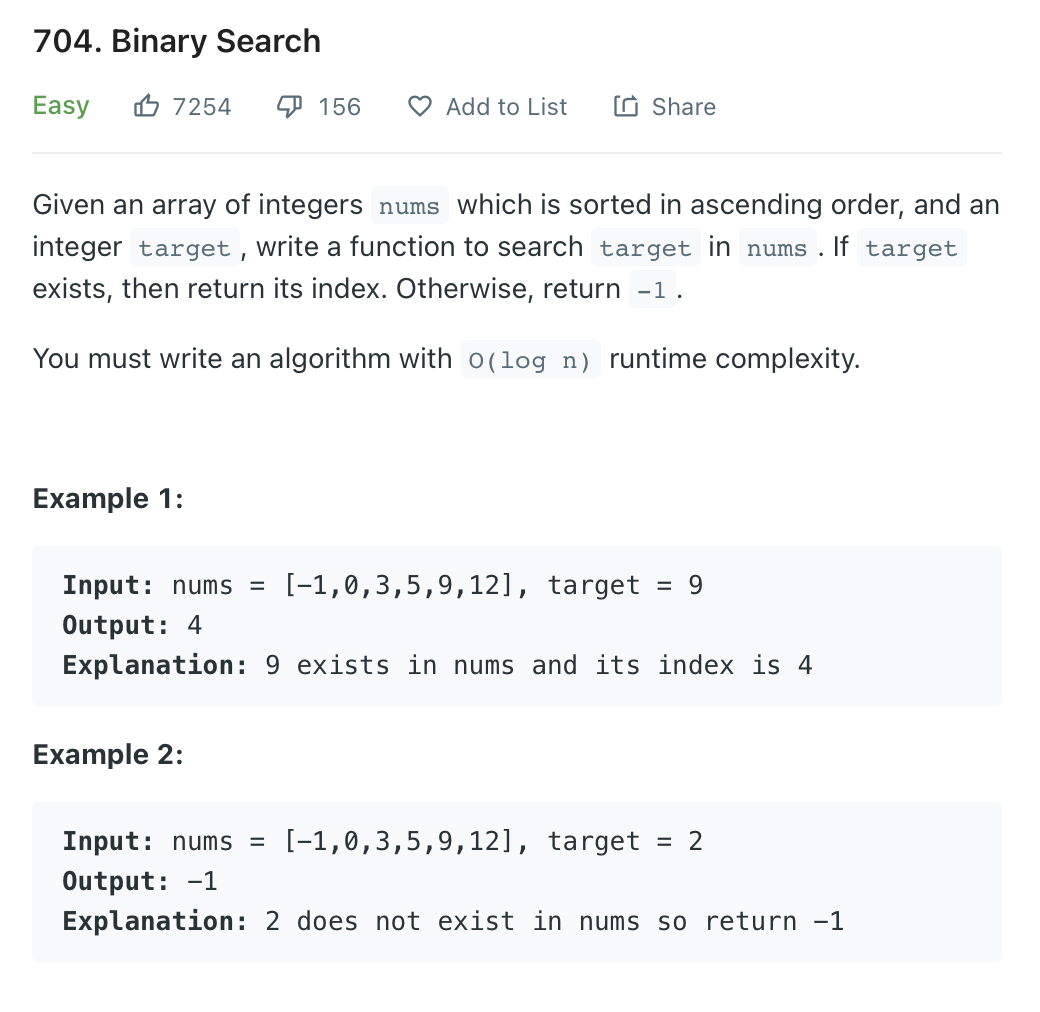
class Solution(object):
def search(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
lo = 0
hi = len(nums) - 1
if (target < nums[0]) or (target > nums[-1]):
return -1
else:
while lo <= hi: # 등호를 포함함으로써 element 가 하나만 남는 상황도 포함할 수 있고
mid = (lo+hi)//2 # 그 경우 mid 는 자기 자신이다.
if target < nums[mid]:
hi = mid-1 # 계속 줄여나가기
elif target > nums[mid]:
lo = mid+1 # 계속 줄여나가기
else: #target == nums[mid]
return mid
return -1
162. Find Peak Element

이 문제가 어려웠던건 peak 는 여러개 존재할 수 있기 때문에 mid 값이 peak 가 아닌 경우에 mid 기준으로 왼쪽, 오른쪽 모두에 peak 가 존재할 가능성이 있다는 것이었다. 최악의 경우에는 모든 가능성을 탐구해야하나 싶은 생각이 들었다. 하지만 큰 값을 따라가다보면 언젠가는 peak 를 찾게 된다는 규칙을 발견했다. 이 규칙을 이용해 문제를 풀었다.
class Solution(object):
def findPeakElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
lo = 0
hi = len(nums)-1
while lo <= hi:
mid = (hi+lo)//2
if lo == hi:
if mid == 0:
return mid
elif mid == len(nums)-1:
return mid
if (nums[mid] > nums[mid-1] and nums[mid] > nums[mid+1]):
return mid
elif (nums[mid] < nums[mid+1]): #move to large direction
lo = mid+1
elif (nums[mid] < nums[mid-1]):
hi = mid-1
153. Find Minimum in Rotated Sorted Array
sorted array 를 다룰땐 꼭 sorted 되었다는 조건을 활용해야한다.

sorted list 라면 최소값이 맨 왼쪽 값일 것이다. 만약 rotated sorted list 라면 unsorted 지점 (위의 예시에서 5였다가 1이 되는 지점)이 최소값이 될 것이다. 항상 unsorted 리스트를 반으로 쪼개면 절반의 두개 리스트중 하나에는 unsorted 지점이 포함될 것이고 이를 탐색해 나가자는게 솔루션 전략이다.
class Solution(object):
def findMin(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
lo = 0
hi = len(nums) - 1
if len(nums) <= 2:
return min(nums)
while lo <= hi:
if nums[lo] < nums[hi]: #it is sorted array
return nums[lo] # return the left most value
else:
mid = int((lo+hi)/2) # take the minimum index
if nums[mid-1] > nums[mid]: # we know for sure this value is minimum
return nums[mid]
elif nums[mid] > nums[hi]: #meaning that it is not sorted array
lo = mid+1 # we have to keep shrinking range
elif nums[lo] > nums[mid]:
hi = mid-1 # we have to keep shrinking range74. Search a 2D Matrix
class Solution(object):
def searchMatrix(self, matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
lo = 0
hi = len(matrix)-1
# search in the leftmost column
i = 0
while lo <= hi: # it has to be lo==hi to include array with a single element
mid = int((lo+hi)/2)
if matrix[mid][0] == target:
return True
elif matrix[mid][0] > target:
hi = mid-1 # we have to keep reducing range
else: # if matrix[mid][0] < target:
i = max(i, mid) #largest index that is smaller than target value
lo = mid+1
left = 0
right = len(matrix[0])-1
while left <= right:
mid = int((left+right)/2)
if matrix[i][mid] == target:
return True
elif matrix[i][mid] > target:
right = mid-1
else: #matrix[i][mid] < target
left = mid+1
return False # if you have not returned True; return False
Linked list
876. Middle of the Linked List

기본 아이디어는 fast 와 slow 두개의 카피를 만들어서 slow 는 한칸씩, fast 는 두칸씩 움직이고 fast 가 맨 마지막에 도달했을때 slow 를 return 하면 가장 중간의 노드를 return 할 수 있다는 것이다.
class Solution(object):
def middleNode(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
slow = fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
return slow19. Remove Nth Node From End of List
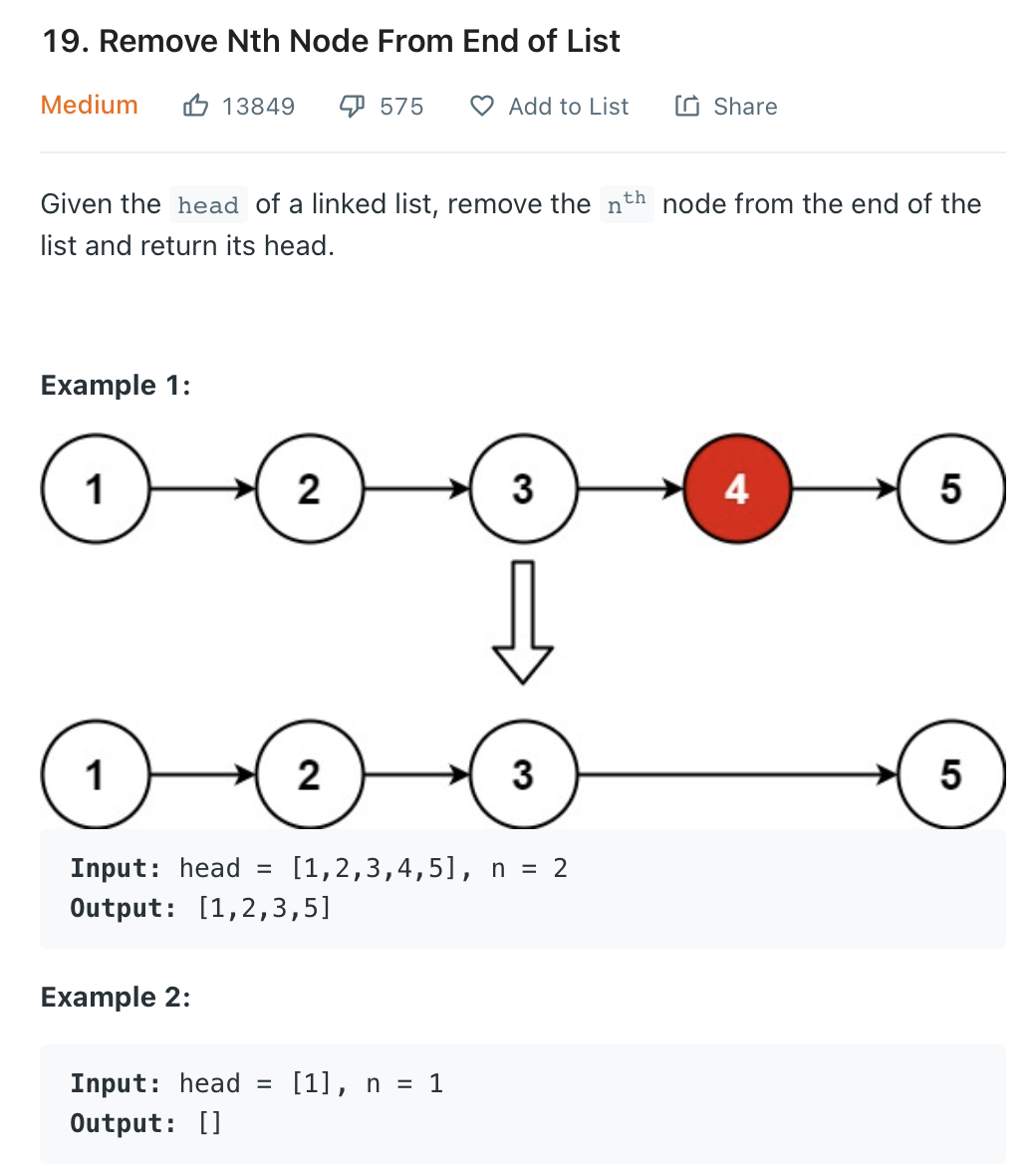
일단 한번 링크드 리스트를 쭉 따라 탐색해서 총 리스트의 크기를 구해낸 다음 k-n-1번째의 next node 를 그의 next node 로 대체한다.
class Solution(object):
def removeNthFromEnd(self, head, n):
"""
:type head: ListNode
:type n: int
:rtype: ListNode
"""
k = 0
count = head
while count:
count = count.next
k += 1
if k == n: # for the corner case when k == n
return head.next # 맨처음 element 를 삭제하는 경우는 별도로 정의해준다.
move = head
for _ in range(k-n-1):
move = move.next
move.next = move.next.next
return head처음에는 head를 return 하는게 이해가 안됐다. 결국 head 는 링크드 리스트의 맨 앞에 있는 하나의 오브젝트다. 그의 next 와 그의 next 의 next 등등이 체인형태로 연결되어있기 때문에 head는 전체 링크드 리스트의 information 을 다 가지고 있다. 우리가 move 를move.next 로 덮어쓰기 하면서 move 는 결국 None 이 되지만 어떤 순간에 특정 노드의 next 를 다른 포인터로 덮어쓰기 하면 그 object 자체가 가지고 있는 next 값이 바뀌기 때문에 마지막에 head 를 리턴했을때 전체 링크드 리스트가 수정되는 것이다.
BFS/DFS
104. Maximum Depth of Binary Tree

어차피 모든 노드를 탐색해야하는거라 bfs/dfs 상관 없음.
class Solution(object):
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None:
return 0
queue = [] #bfs solution
depth = [1] # keep track of depth
queue.append(root)
while queue: # while queue is not None
current = queue.pop(0)
current_depth = depth.pop(0)
if current.left:
queue.append(current.left)
depth.append(current_depth+1)
if current.right:
queue.append(current.right)
depth.append(current_depth+1)
return current_depth112.Path Sum (Linked list 문제와도 연관됨)
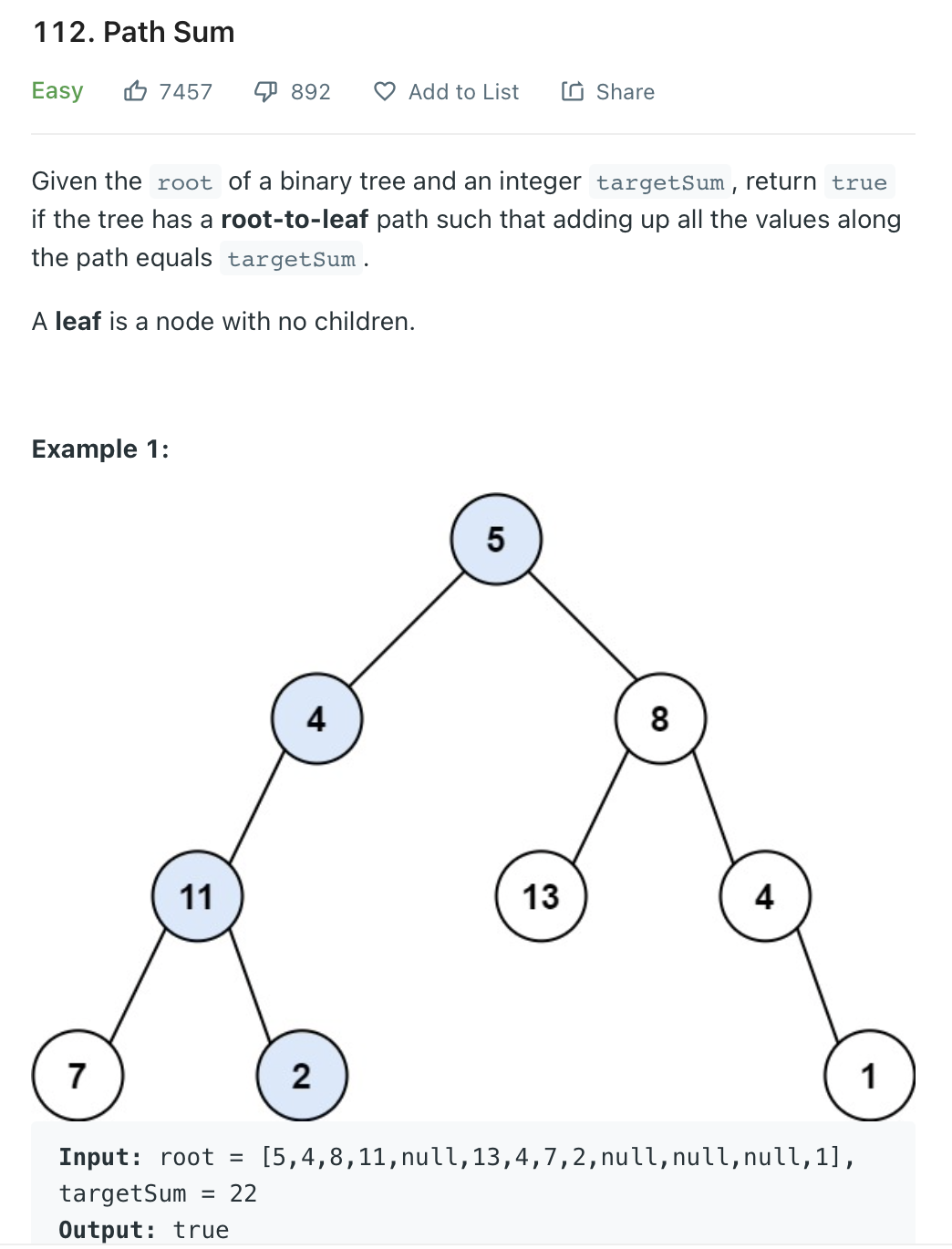
targetSum 을 만족시키는 path 를 하나라도 찾으면 true 를 리턴하면 되므로 dfs 가 조금 더 적절
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if root is None:
return False
target_sum = [root.val] # 노드 탐색과 동시에 target sum 을 저장해나가는게 포인트
stack = [root]
while stack:
current = stack.pop()
current_sum = target_sum.pop()
if current.left:
stack.append(current.left)
current_sum_left = current_sum
current_sum_left += current.left.val
target_sum.append(current_sum_left)
if current.right:
stack.append(current.right)
current_sum_right = current_sum
current_sum_right += current.right.val
target_sum.append(current_sum_right)
if (current.left is None) and (current.right is None):
if current_sum == targetSum:
return True
return False117. Populating Next Right Pointers in Each Node II

같은 레벨에 있는 애들끼리 이어줘야하므로 bfs 가 더 적절함
class Solution(object):
def connect(self, root):
"""
:type root: Node
:rtype: Node
"""
queue = [root]
while queue:
new_queue = []
for node in queue:
if node is not None: # handling corner case: [None]
if node.left:
new_queue.append(node.left)
if node.right:
new_queue.append(node.right)
if new_queue:
for i in range(len(new_queue)-1):
new_queue[i].next = new_queue[i+1] # access to Node and set next
queue = new_queue
return root
200. Number of Islands

어떤 한점에서 시작해 연결되는 path 가 존재하면 그것은 island 로 판단한다. 방문과 동시에 cell 의 값을 "0"으로 수정해 중복되는 일이 없도록 하는게 포인트였다.
class Solution(object):
def numIslands(self, grid):
"""
:type grid: List[List[str]]
:rtype: int
"""
m = len(grid)
n = len(grid[0])
count = 0
def bfs(i, j): # input is starting position
queue = deque()
queue.append((i,j))
while queue:
(i,j) = queue.popleft()
grid[i][j] = 0 # record cell is visited
if (i-1 >= 0):
if (grid[i-1][j] == "1"): #move left
queue.append((i-1, j))
if (i+1 <= m-1):
if (grid[i+1][j] == "1"): #move right
queue.append((i+1, j))
if (j-1 >= 0):
if (grid[i][j-1] == "1"): # move up
queue.append((i, j-1))
if (j+1 <= n-1):
if (grid[i][j+1] == "1"): # move down
queue.append((i, j+1))
for i in range(m):
for j in range(n):
if grid[i][j] == "1":
count += 1
bfs(i, j)
return count
785. Is Graph Bipartite?
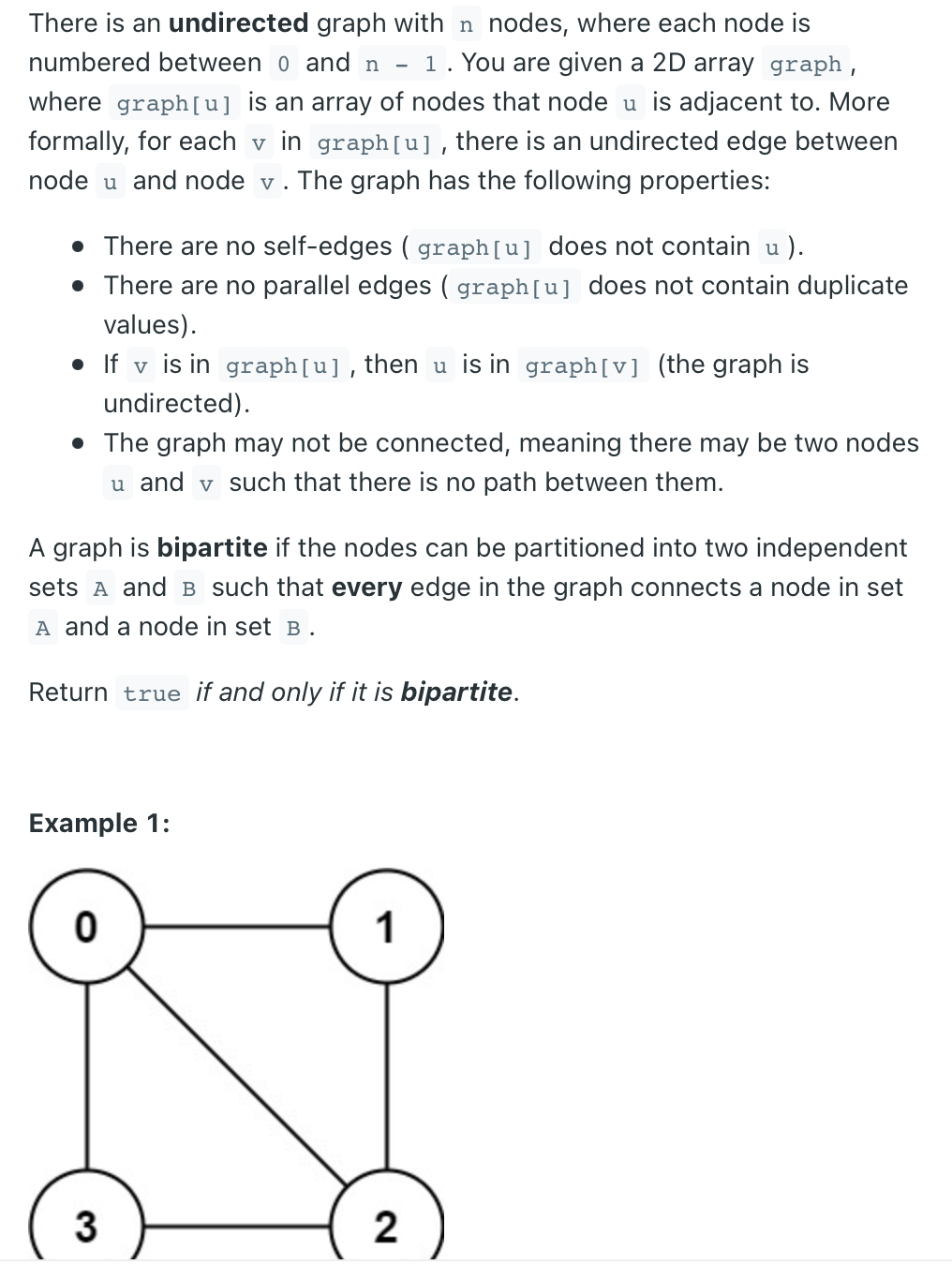
문제를 읽고 풀이 방법을 생각해내는게 어려웠던 문제. 한 노드를 set A로 할당하면 그 neighbors 는 모두 set B 에 있어야한다. dfs를 사용하면 연결된 모든 노드를 탐색하면서 그 사실관계를 탐색 할 수 있다. 여러개의 bipartite graph 가 나올 수도 있는데 처음 만나는 node 를 set A, B 어느쪽으로 할당하든 무관하다.
class Solution(object):
def isBipartite(self, graph):
"""
:type graph: List[List[int]]
:rtype: bool
"""
n = len(graph)
visited = [-1 for _ in range(n)] # -1: unvisited, A, B
for u in range(n):
if visited[u] != -1:
continue
else:
stack = [u]
visited[u] = 'A'
while stack:
i = stack.pop()
for v in graph[i]: #get neighbors
if visited[v] != -1: # if the neighbors already visited
if visited[v] == visited[i]: # if the neighbor is in the same set
return False
continue
else:
if visited[i] == 'A':
visited[v] = 'B'
else: #visited[i] == 'B':
visited[v] = 'A'
stack.append(v)
return True
Backtracking
Backtracking is an algorithmic technique for solving problems recursively by trying to build a solution incrementally, one piece at a time, removing those solutions that fail to satisfy the constraints of the problem at any point of time (by time, here, is referred to the time elapsed till reaching any level of the search tree).
Brute force way 를 가장 먼저 생각해야한다. Decision tree를 그려본다.
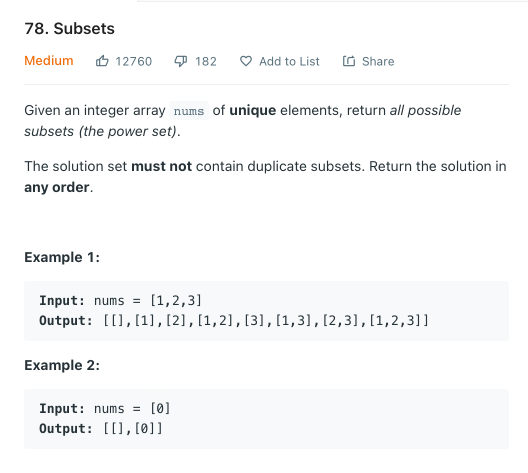
78. Subsets
class Solution(object):
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
power_set = [[]]
for e in nums: # 리스트의 모든 요소를 돌면서
new_power_set = []
for l in power_set:
new_power_set.append(l) # element 를 포함 안하는 경우
new_power_set.append(l + [e]) #element 를 포함하는 경우로 branching
power_set = new_power_set
return power_set
90. Subsets II
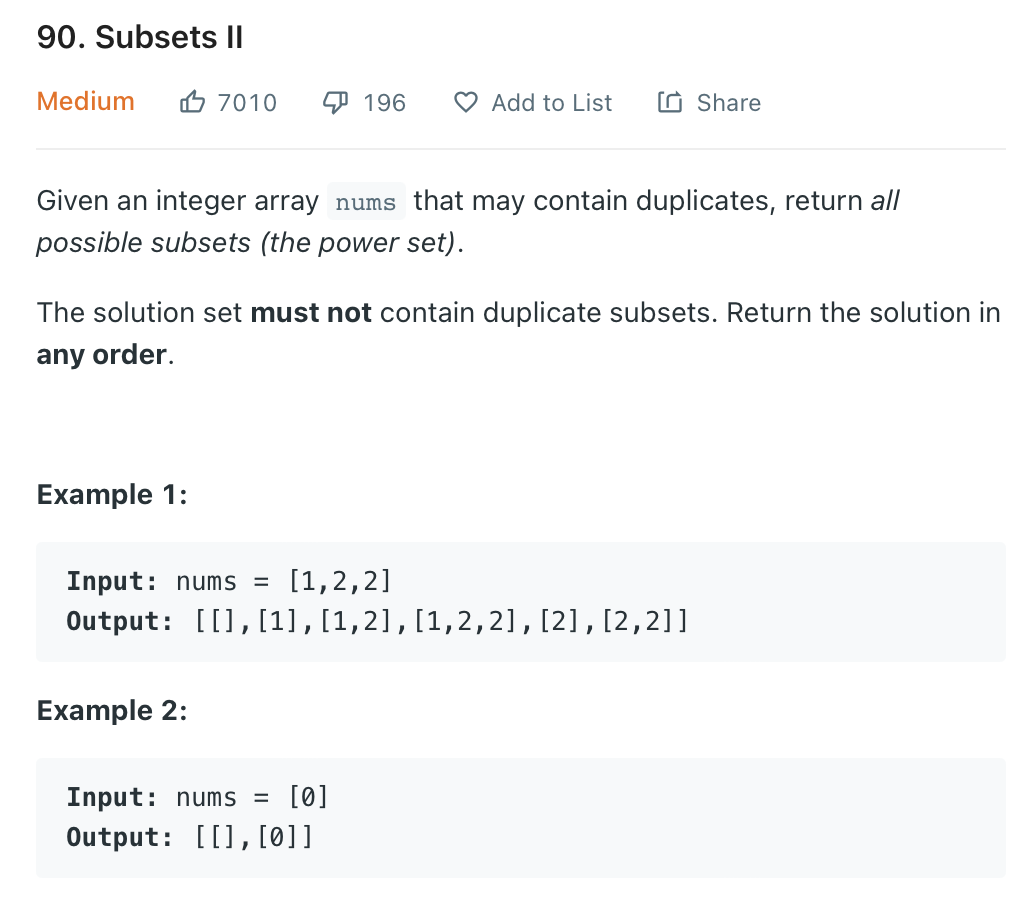
중복이 되는 숫자들이 있기 때문에 앞선 솔루션을 그대로 활용하면 문제가 생긴다. 예를들어 첫번째 두번째 요소를 포함하는 경우와 첫번째 세번째 요소를 포함하는 경우가 모두 [1,2] 로 중복이 발생한다. 이 문제를 해결하기 위해 hash map 을 사용한다. 각 element 의 unique 한 개수를 먼저 세는 것이다.
class Solution(object):
def subsetsWithDup(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
unique_num = {}
for e in nums:
if e not in unique_num: # if the element does not yet exist in the key
unique_num[e] = 1
else:
unique_num[e] = unique_num[e] +1
power_set = [[]]
for e in unique_num:
new_power_set = []
for l in power_set:
for n in range(unique_num[e]+1):
new_power_set.append(l + [e]*n)
power_set = new_power_set
return power_set
216. Combination Sum III

두가지 방식의 코딩을 해볼 수 있다. element 를 1부터 9까지 탐색하면서 1을 포함해?말아? 2를 포함해?말아? ... 이런식으로 두갈래씩 뻗어나가며 조건이 맞지 않을때 탐색을 중단하는 식으로 backtracking 을 할 수 있다.
class Solution(object):
def combinationSum3(self, k, n):
"""
:type k: int
:type n: int
:rtype: List[List[int]]
"""
valid_comb = list()
def sub(target, e, comb):
# target: n으로 시작해서 element 를 list 에 추가할 때마다 그 크기만큼 줄어듬
# comb: empty list 로 시작해서 element 를 더해나감
if (target == 0) and (len(comb) == k):
#그동안 더한 element 가 k개 이고 합이 target과 같을때 return 할 list 에 더한다
valid_comb.append(comb)
elif target > 0: # keep doing
if (e <= target) and (e <= 9) and (len(comb) < k):
# 더하려는 element 가 target 보다 작을경우, element 1부터 9까지
# 지금까지 더한 element 수가 아직 k 개 보다 작을때
sub(target-e, e+1, comb + [e])
sub(target, e+1, comb)
sub(n, 1, list())
return valid_comb
Dynamic Program
Dynamic programming 문제를 접근하는 것은 1) 문제속에 숨겨진 재귀함수를 발견하고 recursion 으로 풀기. 이는 기본적으로 brute-force 방식이라 효율적이지 못하다 2) memoization with top-down 3) bottom up. Memoization 을 위해서는 1d 혹은 2d array 를 정의해서 subproblem을 처음 풀었다면 값을 저장하고, 이미 값이 저장되어있다면 다시 풀지 않고 저장된 값을 활용하는 것이다. 솔루션이 명확하게 보이지 않을땐 decision tree 를 그려 가능한 모든 경우의 수를 그려보고 겹치는 연산이 뭐가 있을지를 따져보는 것이 좋다.
62. Unique Paths

2d array 를 잘 활용해야하는 문제이다. array indexing 에 유의하자. subproblem 을 각 셀마다 정의해서 이 셀까지 도달할 수 있는 unique path 의 수를 구한다. 이로부터 재귀 함수를 정의할 수 있다. backward 로 구한 솔루션이다.
class Solution(object):
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
unique_path = [[0 for _ in range(n+1)] for _ in range(m+1)]
unique_path[m-1][n-1] = 1
for i in range(m-1, -1, -1):
for j in range(n-1, -1, -1):
if (i == m-1) and (j == n-1):
continue
else: unique_path[i][j] = unique_path[i][j+1] + unique_path[i+1][j]
return unique_path[0][0]63. Unique Paths II

이 또한 backward 로 구한 솔루션이다. 위의 문제를 backward 로 접근하지 않았으면 문제가 복잡해 졌을텐데 위에껄 backward 로 풀었기 때문에 간편했다.
class Solution(object):
def uniquePathsWithObstacles(self, obstacleGrid):
"""
:type obstacleGrid: List[List[int]]
:rtype: int
"""
m = len(obstacleGrid)
n = len(obstacleGrid[0])
if obstacleGrid[m-1][n-1] == 1:
return 0
unique_path = [[0 for _ in range(n+1)] for _ in range(m+1)]
unique_path[m-1][n-1] = 1
for i in range(m-1, -1, -1):
for j in range(n-1, -1, -1):
if (i == m-1) and (j == n-1):
continue
elif obstacleGrid[i][j] == 1:
unique_path[i][j] = 0
else: unique_path[i][j] = unique_path[i][j+1] + unique_path[i+1][j]
return unique_path[0][0]
References
Technical interview cheat sheet: https://gist.github.com/TSiege/cbb0507082bb18ff7e4b
Leetcode: https://leetcode.com/problemset/all/
How come the time complexity of Binary Search is log n : https://math.stackexchange.com/questions/3224473/how-come-the-time-complexity-of-binary-search-is-log-n
'미국 테크기업 인턴쉽' 카테고리의 다른 글
| 아마존 박사과정 여름방학 리서치 인턴십 준비 과정 (0) | 2024.03.20 |
|---|---|
| 아마존 박사과정 여름방학 리서치 인턴쉽 두번째 인터뷰 후기 (1) | 2022.11.30 |
| Uber PhD Applied Scientist Internship 1차 폰 스크리닝 인터뷰 후기 (1) | 2022.11.22 |
| 아마존 박사과정 여름방학 리서치 인턴쉽 첫번째 인터뷰 후기 (0) | 2022.11.17 |